from skimage import io
import matplotlib.pyplot as plt
import numpy as np

Lineare Nachbarschaftsfilter

Aufgabe 2

Faltet ein Bild mit einer Filtermatrix ohne spezielle Randbehandlung

def simple_filter(in_image, filter_matrix, offset=1):
    img_h, img_w = in_image.shape
    filter_size = filter_matrix.shape[0]
 
    out_h = (img_h - filter_size) // offset + 1
    out_w = (img_w - filter_size) // offset + 1
    out_image = np.zeros((out_h, out_w), dtype=int)
 
    for i in range(out_h):
        for j in range(out_w):
            sum_value = 0.0
            for u in range(filter_size):
                for v in range(filter_size):
                    xi = i * offset + u
                    yj = j * offset + v
                    if 0 <= xi < img_h and 0 <= yj < img_w:
                        sum_value += in_image[xi, yj] * filter_matrix[u, v]
            out_image[i, j] = np.clip(int(sum_value), 0, 255)
 
    return out_image

def get_pixel(in_image, x, y, edge='min'):
 
    img_h, img_w = in_image.shape
    if 0 <= x < img_h and 0 <= y < img_w:
        return in_image[x, y]
    else:
        if edge == 'min':
            return 0
        elif edge == 'max':
            return 255
        elif edge == 'continue':
            x = min(max(x, 0), img_h - 1)
            y = min(max(y, 0), img_w - 1)
            return in_image[x, y]
        else:
            raise ValueError(f"Unbekannte Randbehandlung: {edge}")

Aufgabe 3

Faltet ein Bild mit einer Filtermatrix und behandelt die Ränder entsprechend ‘min’, ‘max’ oder ‘continue’

def advanced_filter(in_image, filter_matrix, offset=1, edge='continue'):
    img_h, img_w = in_image.shape
    filter_size = filter_matrix.shape[0]
    k = filter_size // 2  # half filter size
 
    out_h = (img_h - 1) // offset + 1
    out_w = (img_w - 1) // offset + 1
    out_image = np.zeros((out_h, out_w), dtype=int)
 
    for i in range(out_h):
        for j in range(out_w):
            sum_value = 0.0
            center_x = i * offset
            center_y = j * offset
            for u in range(filter_size):
                for v in range(filter_size):
                    xi = center_x + (u - k)
                    yj = center_y + (v - k)
                    pixel = get_pixel(in_image, xi, yj, edge)
                    sum_value += pixel * filter_matrix[u, v]
            out_image[i, j] = np.clip(int(sum_value), 0, 255)
 
    return out_image

def plot_images(images, titles=None, rows=1):
    cols = int(np.ceil(len(images) / rows))  # Calculate the number of columns
    fig, axes = plt.subplots(rows, cols, figsize=(15, 10))
    axes = np.array(axes).reshape(-1)  # Flatten axes for easy iteration
 
    for i, img in enumerate(images):
        axes[i].imshow(img, cmap='gray')
        if titles:
            axes[i].set_title(titles[i])
        axes[i].axis('off')
 
    # Hide any unused subplots
    for j in range(len(images), len(axes)):
        axes[j].axis('off')
 
    plt.tight_layout()
    plt.show()

Testbilder

img = np.random.randint(0, 256, (10, 10), dtype=int)
 
filter_matrix = np.array([
    [1, 1, 1],
    [1, 3, 1],
    [1, 1, 1]
], dtype=float) / 11
 
out_simple = simple_filter(img, filter_matrix, offset=1)
 
plot_images([img, out_simple], titles=['Original', 'Einfacher Filter'])

png

img = np.full((10, 10), 255, dtype=int)
 
img[3:7, 3:7] = 0
 
filter_matrix = np.array([
    [1, 1, 1],
    [1, 3, 1],
    [1, 1, 1]
], dtype=float) / 11
 
out_min = advanced_filter(img, filter_matrix, offset=1, edge='min')
out_max = advanced_filter(img, filter_matrix, offset=1, edge='max')
out_continue = advanced_filter(img, filter_matrix, offset=1, edge='continue')
 
plot_images([img, out_min, out_max, out_continue],
             titles=['Original', 'min', 'max', 'continue'])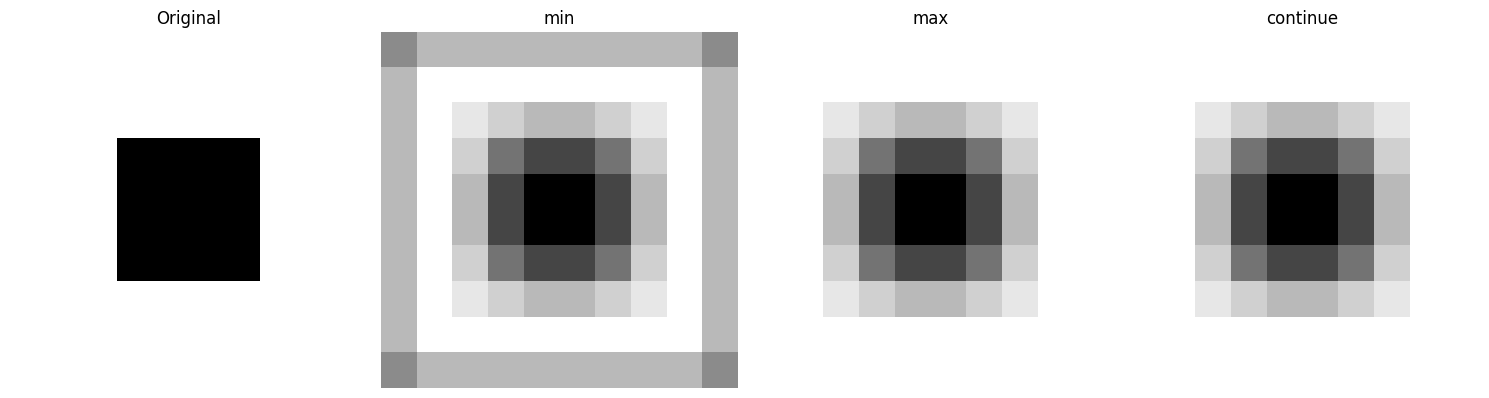

png

img = io.imread('lena.jpg', as_gray=True)
img = (img * 255).astype(int)
 
filters = {
    'sharp' : np.array([
        [0, -1, 0],
        [-1, 5, -1],
        [0, -1, 0]
    ], dtype=float),
    'box' : np.array([
        [1, 1, 1],
        [1, 1, 1],
        [1, 1, 1]
    ], dtype=float) / 9,
    'gaussian' : np.array([
        [1, 2, 1],
        [2, 4, 2],
        [1, 2, 1]
    ], dtype=float) / 16,
    'laplace' : np.array([
        [0, -1, 0],
        [-1, 4, -1],
        [0, -1, 0]
    ], dtype=float),
    'sobel' : np.array([
        [-1, 0, 1],
        [-2, 0, 2],
        [-1, 0, 1]
    ], dtype=float)
}
 
out_images = [img]
titles = ['Original']
 
for name, filter_matrix in filters.items():
    out_image = advanced_filter(img, filter_matrix, offset=1, edge='continue')
    out_images.append(out_image)
    titles.append(name)
 
plot_images(out_images, titles=titles, rows=2)

png

a) Nennen Sie die Arten und Eigenschaften von linearen Filtern

Arten von linearen Filtern:
- Gaussian-Filter
- Sobel-Filter
- Laplace-Filter
Eigenschaften von linearen Filtern:
- Linearität: Die Ausgabe ist eine lineare Kombination der Eingabewerte.
  - $F (a \cdot I 1 + b \cdot I 2) = a \cdot F (I 1) + b \cdot F (I 2)$
- Zeitinvarianz: Die Filtereigenschaften ändern sich nicht mit der Zeit.
  - $F (I (t)) = F (I) (t)$
- Stabilität: Kleine Änderungen in den Eingabewerten führen zu kleinen Änderungen in den Ausgabewerten.
  - $∣ F (I 1) - F (I 2) ∣ \leq k \cdot ∣ I 1 - I 2∣$ für eine Konstante k
- Kausalität: Der Filter reagiert nur auf aktuelle und vergangene Eingabewerte, nicht auf zukünftige Werte.
  - $F (I (t)) = F (I (t - 1), I (t - 2), ...)$

b) Was ist der Unterschied zwischen linearen und nichtlinearen Filtern?

Kriterium	Lineare Filter	Nichtlineare Filter
Mathematische Eigenschaft	Linear: Addition und Skalierung bleibt erhalten	Nichtlinear: Addition und Skalierung funktionieren nicht so
Beispiele	Mittelwertfilter, Sobel-Filter	Medianfilter, Min/Max-Filter
Typisches Verhalten	Verwischen von Rauschen, Kantenglättung	Entfernung von Ausreißern (z.B. Salt & Pepper Noise)
Operation	Faltung (Summe von gewichteten Pixeln)	Sortieren, Maximum, Median, andere nichtlineare Berechnungen
Vorteil	Einfach zu berechnen, schnelle Filterung	Besser bei impulsartigem Rauschen (z.B. Störpixel)
Nachteil	Kann Kanten verwischen	Aufwendigere Berechnung, komplexere Mathematik

Nichtlineare Nachbarschaftsfilter

Holt den Pixelwert mit Randbehandlung (hier: 0 außerhalb)

def get_pixel_median(in_image, x, y):
    img_h, img_w = in_image.shape
    if 0 <= x < img_h and 0 <= y < img_w:
        return in_image[x, y]
    else:
        return 0  # Zero padding (min)
 
get_pixel_median(img, 0, 0)

np.int64(154)

Sammelt alle Pixel in der Umgebung (Neighborhood) um (center_x, center_y)

def get_neighborhood(in_image, center_x, center_y, filtersize):
    k = filtersize // 2
    neighborhood = []
 
    for u in range(filtersize):
        for v in range(filtersize):
            xi = center_x + (u - k)
            yj = center_y + (v - k)
            pixel = get_pixel_median(in_image, xi, yj)
            neighborhood.append(pixel)
 
    return neighborhood
 
get_neighborhood(img, 5, 5, 3)  # Test neighborhood function

[np.int64(153),
 np.int64(153),
 np.int64(153),
 np.int64(152),
 np.int64(152),
 np.int64(152),
 np.int64(151),
 np.int64(150),
 np.int64(150)]

Berechnet den Median eines gegebenen Neighborhoods (Pixelwerte)

def compute_median(neighborhood):
    neighborhood.sort()
    median_value = neighborhood[len(neighborhood) // 2]
    return median_value
 
compute_median([1, 6, 3, 9, 4])  # Test median function

Hauptfunktion: Wendet Medianfilter mit gegebenem filtersize und offset an

def medianFilter(in_image, filtersize, offset=1):
    img_h, img_w = in_image.shape
    out_h = (img_h - 1) // offset + 1
    out_w = (img_w - 1) // offset + 1
    out_image = np.zeros((out_h, out_w), dtype=int)
 
    for i in range(out_h):
        for j in range(out_w):
            center_x = i * offset
            center_y = j * offset
            neighborhood = get_neighborhood(in_image, center_x, center_y, filtersize)
            median_value = compute_median(neighborhood)
            out_image[i, j] = median_value
 
    return out_image

img = np.random.randint(0, 256, (10, 10), dtype=int)
 
filtered_img = medianFilter(img, filtersize=3, offset=1)
 
plot_images([img, filtered_img], titles=['Original', 'Median-Filter'])

png

image_files = ['tree.png', 'pepper.jpg']
 
for image_file in image_files:
    img = io.imread(image_file)
 
    filter_sizes = range(2, 5)
    filtered_images = [medianFilter(img, filtersize=fsize, offset=1) for fsize in filter_sizes]
 
    plot_images([img] + filtered_images,
                titles=[f'{image_file} - Original'] + [f'Filter size: {fsize}' for fsize in filter_sizes])

png

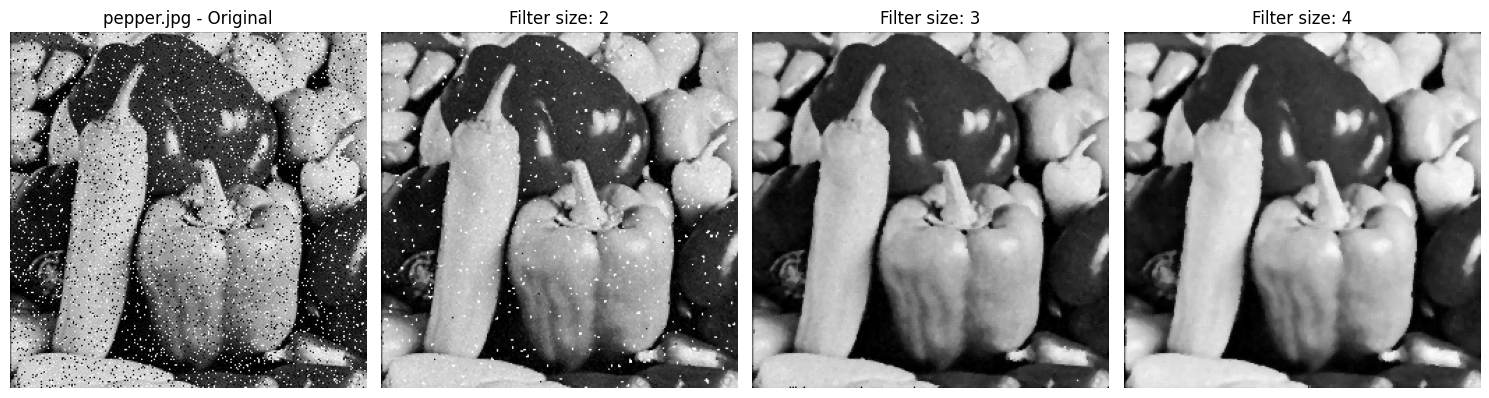
a) Vergleichen Sie die Ergebnisse der verschiedenen Filter miteinander und begründen Sie diese.

Lineare Filter:
- Glätten das Bild, indem sie Pixelwerte mitteln.
- Reduzieren gleichmäßiges Rauschen.
- Problem: Kanten werden dabei oft unscharf oder verschwimmen, weil auch starke Pixelunterschiede gemittelt werden.
Nichtlineare Filter:
- Ersetzen einen Pixel durch den Medianwert seiner Nachbarn.
- Sehr gut bei impulsartigem Rauschen (z.B. Salt & Pepper Noise).
- Vorteil: Kanten bleiben besser erhalten, weil der Median extreme Ausreißer ignoriert.

b) Warum ist es beim Medianfilter sinnvoll für die Sortierung Heap Sort zu verwenden?

Heap Sort ist effizient, da es auch bei großen Nachbarschaften eine gute Laufzeit $(O (n lo g n))$ hat und wenig Speicherplatz benötigt.
Weil beim Medianfilter nicht die vollständige Sortierung aller Werte nötig ist, eignet sich Heap Sort besonders gut.

c) Untersuchen Sie, welche Effekte bei mehrmaligem Anwenden eines Filters auf das jeweilige Ergebnisbild auftreten.

Bei mehrmaliger Anwendung eines Filters wird das Bild zunehmend geglättet.
Details und feine Strukturen verschwinden nach und nach, bei Medianfiltern bleiben Kanten zunächst erhalten, werden aber mit der Zeit breiter und weicher.

d) Welche Effekte treten bei grossen und bei kleinen Filtermasken auf?

Kleine Filtermasken erhalten Details besser und glätten nur leichtes Rauschen.
Große Masken sorgen für starke Glättung und entfernen auch starkes Rauschen, führen aber dazu, dass Kanten und Details verloren gehen.

🦉 Main

Explore

Aufgabe 3

Lineare Nachbarschaftsfilter

Aufgabe 2

Aufgabe 3

Testbilder

a) Nennen Sie die Arten und Eigenschaften von linearen Filtern

b) Was ist der Unterschied zwischen linearen und nichtlinearen Filtern?

Nichtlineare Nachbarschaftsfilter

a) Vergleichen Sie die Ergebnisse der verschiedenen Filter miteinander und begründen Sie diese.

b) Warum ist es beim Medianfilter sinnvoll für die Sortierung Heap Sort zu verwenden?

c) Untersuchen Sie, welche Effekte bei mehrmaligem Anwenden eines Filters auf das jeweilige Ergebnisbild auftreten.

d) Welche Effekte treten bei grossen und bei kleinen Filtermasken auf?

Zuletzt bearbeitete Seiten

Studium

🧑🏼‍💻 Probeklausur

Code Beispiele

Graphansicht

Inhaltsverzeichnis