Main

Aufgabe 4

4 min read

Beantworten Sie folgende Fragen:

Was ist eine Kante und wie ist sie im Bild, in dessen Ableitung erkennbar?

Eine Kante ist ein Bildbereich, in dem sich die Helligkeit stark verändert. In der Ableitung des Bildes entspricht dies einem Punkt, an dem die Intensitätsänderung (Gradient) ein Maximum hat. Solche Stellen zeigen sich als Extremwerte in der ersten Ableitung oder als Nulldurchgänge in der zweiten Ableitung

Was sind die partiellen Ableitungen eines Bildes? Was sagen sie aus?

Partielle Ableitungen beschreiben die Helligkeitsänderung entlang der Achsen (horizontal und vertikal ). Sie geben an, wie stark und in welche Richtung sich die Helligkeit des Bildes verändert

Was ist der Gradientenvektor (kurz: Gradient) eines Bildes?

Der Gradient ∇I ist ein Vektor bestehend aus den beiden partiellen Ableitungen. Er zeigt die Richtung des stärksten Helligkeitsanstiegs und seine Länge gibt die Stärke dieses Anstiegs an

Wie kann die Kantenstärke berechnet werden?

Die Kantenstärke wird als Betrag des Gradienten berechnet:

wobei Dx und Dy die Ableitungen in x- und y-Richtung sind.

Wie kann die lokale Kantenrichtung berechnet werden?

Die lokale Kantenrichtung ergibt sich aus dem Winkel:

Sie gibt an, in welcher Richtung die Kante verläuft. Bei der Berechnung sollte die Funktion atan2 verwendet werden, um den Winkelbereich korrekt abzudecken.

sobel.py
import numpy as np
import matplotlib.pyplot as plt
from skimage import io
import time
 
def rgb_2_gray(img, mode='lut'):
    if mode == 'lut':
        return np.round(img[:,:,0] * 0.2126 + img[:,:,1] * 0.7152 + img[:,:,2] * 0.0722)
    else:
        return np.round(img[:,:,0] * 0.2126 + img[:,:,1] * 0.587 + img[:,:,2] * 0.114)
 
 
def sobel(img, filter):
    # Durchführung der 2D-Faltung mit vier verschachtelten Schleifen
    h, w = img.shape
    output = np.zeros((h-2, w-2))
    for i in range(1, h-1):
        for j in range(1, w-1):
            sum = 0
            for u in range(-1, 2):
                for v in range(-1, 2):
                    sum += img[i+u, j+v] * filter[u+1, v+1]
            output[i-1, j-1] = sum
    return output
 
img = io.imread("lena.jpg")
gray = rgb_2_gray(img)
 
height, width = gray.shape
 
# Definition der Sobel-Filter in x- und y-Richtung
filter_x = np.array([[-1, 0, 1],
                     [-2, 0, 2],
                     [-1, 0, 1]])
 
filter_y = np.array([[-1, -2, -1],
                     [ 0,  0,  0],
                     [ 1,  2,  1]])
 
start = time.time()
grad_x = sobel(gray, filter_x)  # Anwendung des Sobel-Filters in x-Richtung
end = time.time()
duration = end-start
print("Dauer in Millisekunden (x): ", duration*1000)
 
start = time.time()
grad_y = sobel(gray, filter_y)  # Anwendung des Sobel-Filters in y-Richtung
end = time.time()
duration = end-start
print("Dauer in Millisekunden (y): ", duration*1000)
 
# Berechnung der Gradientenmagnitude mit der L2-Norm
grad_mag = np.sqrt(grad_x**2 + grad_y**2)
 
# Anzeige der Ergebnisse
plt.figure(figsize=(20, 5))
plt.subplot(1, 4, 1)
plt.title("Originalbild")
plt.imshow(gray, cmap='gray')
 
plt.subplot(1, 4, 2)
plt.title("Gradient X")
plt.imshow(grad_x, cmap='gray')
 
plt.subplot(1, 4, 3)
plt.title("Gradient Y")
plt.imshow(grad_y, cmap='gray')
 
plt.subplot(1, 4, 4)
plt.title("Gradientenbetrag")
plt.imshow(grad_mag, cmap='gray')
plt.show()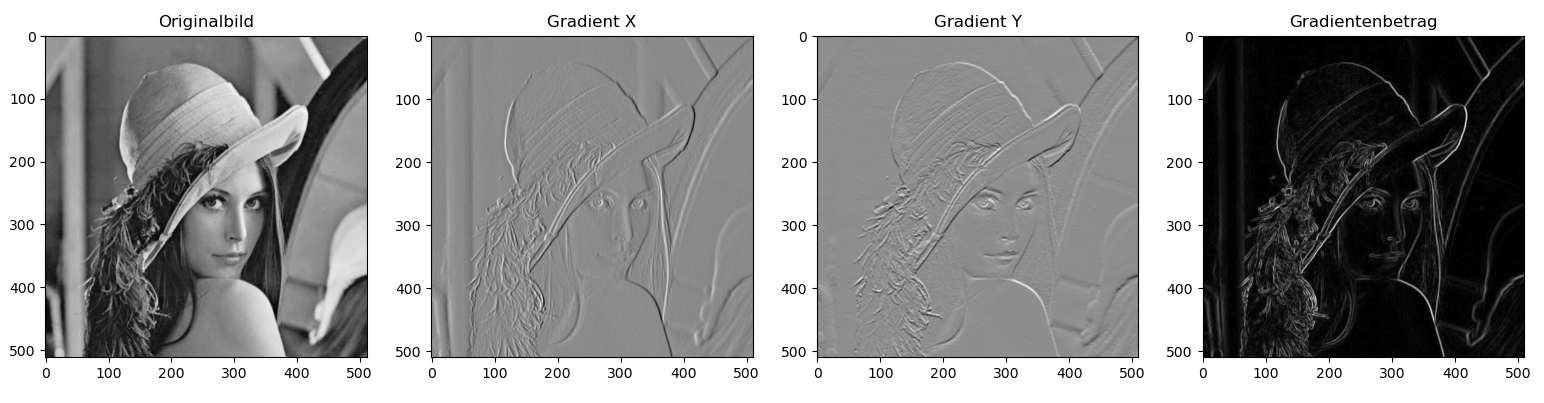

sobel_demo.py
import sobel_demo as nd
import numpy as np
from skimage import io
import matplotlib.pyplot as plt
import time
 
def rgb_2_gray(img, mode='lut'):
    if mode == 'lut':
        return np.round(img[:,:,0] * 0.2126 + img[:,:,1] * 0.7152 + img[:,:,2] * 0.0722)
    else:
        return np.round(img[:,:,0] * 0.2126 + img[:,:,1] * 0.587 + img[:,:,2] * 0.114)
 
img = io.imread("lena.jpg")
gray = rgb_2_gray(img).astype("float64")
 
# Definiere Sobel-Filter in x- und y-Richtung
filter_x = np.array([[-1, 0, 1],
                     [-2, 0, 2],
                     [-1, 0, 1]])
 
filter_y = np.array([[-1, -2, -1],
                     [ 0,  0,  0],
                     [ 1,  2,  1]])
 
start = time.time()
grad_x = nd.sobel(gray, filter_x)  # Filterung in x-Richtung
end = time.time()
print("Dauer in Millisekunden (x):", (end - start) * 1000)
 
start = time.time()
grad_y = nd.sobel(gray, filter_y)  # Filterung in y-Richtung
end = time.time()
print("Dauer in Millisekunden (y):", (end - start) * 1000)
 
# Berechne Gradientenmagnitude
grad_mag = np.sqrt(grad_x**2 + grad_y**2)
 
# Zeige Ergebnisse an
plt.figure(figsize=(20, 5))
plt.subplot(1, 4, 1)
plt.title("Originalbild")
plt.imshow(gray, cmap='gray')
 
plt.subplot(1, 4, 2)
plt.title("Gradient X")
plt.imshow(grad_x, cmap='gray')
 
plt.subplot(1, 4, 3)
plt.title("Gradient Y")
plt.imshow(grad_y, cmap='gray')
 
plt.subplot(1, 4, 4)
plt.title("Gradientenbetrag")
plt.imshow(grad_mag, cmap='gray')
plt.show()
sobel_demo.cpp
#include <pybind11/pybind11.h>
#include <pybind11/numpy.h>
#include <pybind11/eigen.h>
 
namespace py = pybind11;
 
Eigen::MatrixXd sobel(Eigen::MatrixXd gray_img, Eigen::MatrixXd filter)
{
    Eigen::MatrixXd filtered_img(gray_img.rows() - 2, gray_img.cols() - 2);
 
    for (int i = 1; i < gray_img.rows() - 1; ++i)
    {
        for (int j = 1; j < gray_img.cols() - 1; ++j)
        {
            double sum = 0.0;
            for (int u = -1; u <= 1; ++u)
            {
                for (int v = -1; v <= 1; ++v)
                {
                    sum += gray_img(i + u, j + v) * filter(u + 1, v + 1);
                }
            }
            filtered_img(i - 1, j - 1) = sum;
        }
    }
 
    return filtered_img;
}
 
PYBIND11_MODULE(sobel_demo, m)
{
    m.doc() = "sobel operator using numpy!";
    m.def("sobel", &sobel);
}
Messung
$ python3 sobel.py
Dauer in Millisekunden (x):  1258.331298828125
Dauer in Millisekunden (y):  1249.725580215454
$ python3 sobel_demo.py
Dauer in Millisekunden (x): 298.0773448944092
Dauer in Millisekunden (y): 293.5302257537842

Die Implementierung in C++ ist schneller als die in Python, mit einer Laufzeit von 298ms im Vergleich zu 1258ms in Python.

Zuletzt bearbeitete Seiten

Graphansicht