Projective Geometry

Definition

Projective Geometry is a branch of mathematics that studies the properties of geometric objects that are invariant under projective transformations. It extends the concepts of Euclidean geometry by considering points at infinity and the relationships between lines, planes, and higher-dimensional objects.

A Projection is a mapping, that maps a space of dimension $n$ to a space of dimension $<n$.
Because displays and camera are 2d devices, 3d-objects are plotted on them by projecting them onto a 2d plane.

Classification of projections

• Abbreviations:
  • projection ray = p-ray
  • projection plane = p-plane
  • principal axes = p-axes
• Direction of p-ray:
  1. central → relative pose of p-axes to p-plane.
     • Number of intersections of p-axes with p-plane.
  2. parallel → angle of p-ray to p-plane.
     • orthogonal and skew, relative pose of p-axes/-ray to p-plane. Angle of p-axes/-ray to p-plane.

---

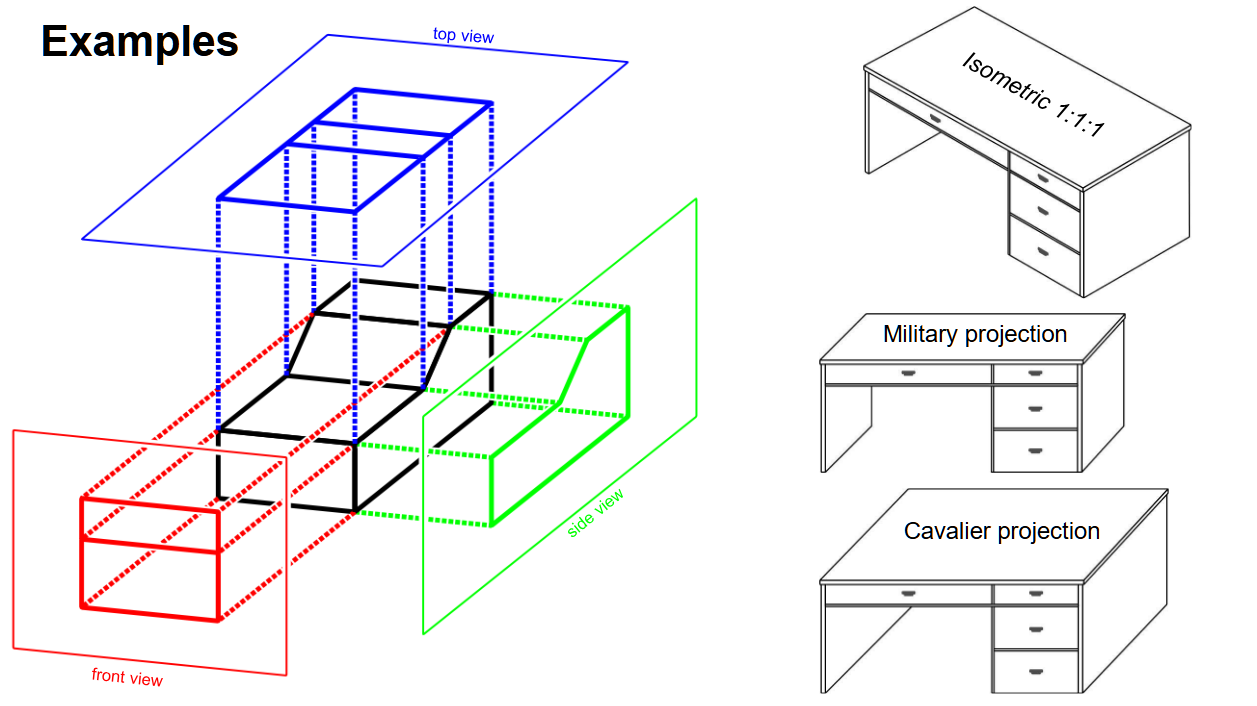
Parallel Projection

• All projection rays are parallel to one direction.
• The centre of projections is a point at infinity.
• Disadvantage: Less realistic.
• Advantage: Allows for exact measurements from the image.
  

---

Perspective Projection (Central Projection)

Perspective projection models how a 3D scene is captured by a pinhole camera (or the human eye). Rays emanate from a single centre of projection and pass through points on the image plane. Distant objects appear smaller; parallel lines converge to vanishing points.

Pinhole Camera Model

Geometry

• centre of projection (camera centre) at O.
• Image plane at distance f (the focal length) in front of O.

Projection Equations

Given a 3D point $(X,Y,Z)$ in camera coordinates $(Z>0)$, its image $(x,y)$ on the image plane at $Z=f$ is

$$x=\frac{fX}{Z},y=\frac{fY}{Z}.$$

Homogeneous Coordinates

Embed $(X,Y,Z)$ and $(x,y)$ into projective space:

$$\left[\begin{array}{c}x\\ y\\ 1\end{array}\right]\propto \underset{P_{\text{int}}}{\underbrace{\left[\begin{array}{cccc}f& 0& 0& 0\\ 0& f& 0& 0\\ 0& 0& 1& 0\end{array}\right]}}\left[\begin{array}{c}X\\ Y\\ Z\\ 1\end{array}\right].$$

• ($P_{\text{int}}$) is the $3\times 4$ intrinsic camera matrix for focal length $f$.

In full generality:

$$K=\left[\begin{array}{ccc}{\alpha }_x& s& c_x\\ 0& {\alpha }_y& c_y\\ 0& 0& 1\end{array}\right],P=K[R\mid \mathbf{t}],$$

where

• ${\alpha }_x=f{m}_x,{\alpha }_y=f{m}_y$ (focal length $\times$ pixel scales),
• $s$ = skew,
• $(c_x,c_y)$ = principal point,
• $[R\mid \mathbf{t}]$ = extrinsic rotation and translation from world to camera.

Intrinsic & Extrinsic Parameters

• Extrinsic $[R\mid \mathbf{t}]$: maps world point ${\mathbf{X}}_w$ to camera frame ${\mathbf{X}}_c=R{\mathbf{X}}_w+\mathbf{t}$.
• Intrinsic $K$: maps camera-frame ${\mathbf{X}}_c$ to image coordinates.

Full mapping in homogeneous coordinates:

$$\left[\begin{array}{c}u\\ v\\ 1\end{array}\right]\propto K[R\mid \mathbf{t}]\left[\begin{array}{c}{X}_w\\ Y_w\\ Z_w\\ 1\end{array}\right].$$

Key Properties & Effects

• Depth division: projection is nonlinear in $(X,Y,Z)$ because of division by $Z$.

• Vanishing points: a 3D direction $\mathbf{d}=(d_x,d_y,d_z)$ projects to

  $$\left(\begin{array}{c}u\\ v\end{array}\right)=\left(\begin{array}{c}\frac{{\alpha }_x{d}_x+s{d}_y}{d_z}+c_x\\ \frac{{\alpha }_y{d}_y}{d_z}+c_y\end{array}\right).$$

• Straight lines in 3D map to straight lines in the image (since projection is linear in homogeneous coords).

• Parallel lines in space meet at the same vanishing point.

Common Exam Questions

1. Derive the perspective equations $x=fX/Z,y=fY/Z$.
2. Explain why projection is not an affine transform.
3. Define the camera matrix $P$ and its decomposition $P=K[R\mid \mathbf{t}]$.
4. Show how a 3D line or plane is mapped under perspective projection.
5. Compute the vanishing point for a given direction vector.
6. Discuss how intrinsic parameters affect the image.

Example: Vanishing Point of the x-axis

For direction $\mathbf{d}=(1,0,0),as{d}_z\to 0$ the image point $(u,v)$ tends to

$$u\to \underset{d_z\to 0}{\lim }\frac{{\alpha }_{x}1+s\cdot 0}{d_z}+c_x=\infty ,v=c_y.$$

So all lines parallel to the x-axis converge to the horizontal line $v=c_y$.

Exam Tips

• Draw the camera centre, object point, image plane, and projection ray.
• Explain each parameter: $f$ controls magnification; $(c_x,c_y)$ shifts the image centre; s handles sensor skew.
• Contrast with orthographic (parallel) projection, where you omit division by $Z$.
• Highlight that recovering 3D from a single image is only possible up to an unknown scale (depth ambiguity).