Klausurvorbereitung

Folgen

Die geordnete Menge aller Werte der Folge bezeichnen wir mit:

$$(a_n{)}_{n\in \mathbb{N}}:(a_1,a_2,a_3,...,a_k,...)$$

---

Konvergenz und Grenzwert einer Folge mit $a$ = Grenzwert und $ϵ\approx 0$ gilt:

$$|a_n-a|<ϵ$$

Eigenschaften von Folgen:

Eine konvergente Folge besitzt genau einen Grenzwert.
Monoton wachsende und nach oben beschrankte Folgen sind konvergent.
Monoton fallende und nach unten beschrankte Folgen sind konvergent.
Konvergente Folgen sind beschränkt.

Funktionen

Injektivität, Surjektivität und Bijektivität

Eine Funktion ist Injektiv, wenn jedes Element der Zielmenge höchstens einmal als Funktionswert auftritt.
Eine Funktion ist surjektiv, wenn jedes Element der Zielmenge mindestens einmal erreicht wird, und bijektiv, wenn sie sowohl injektiv als auch surjektiv ist.

$p(x)=x^r$	$u(x)=a^x$	$v(x)=sinx$
$Potenzfunktion$	$Exponentialfunktion$	$Sinusfunktion$

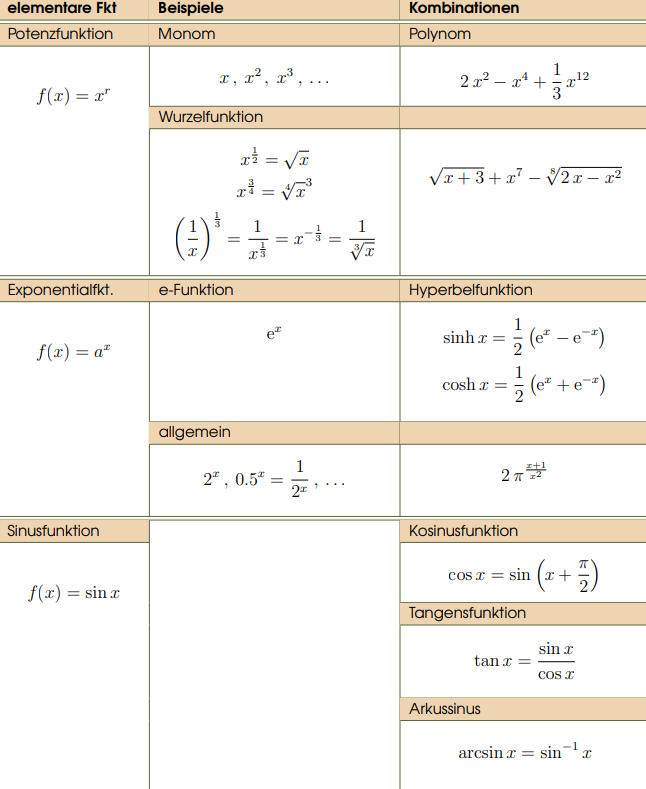
Schreibweise	Definition/Sprechweise
y=f(x)	heißt Funktionswert von $f$ an der Stelle $x$.
A	heißt Definitionsbereich von $f$ (auch ${\mathbb{D}}_f$).
B	heißt Wertebereich von f.
Für $A^{\prime }\subseteq A,B^{\prime }\subseteq B$	heißt
$f(A^{\prime })$	$:=y\in B|\exists x\in A^{\prime }mity=f(x)$ $Bild(-menge)von{A}^{\prime }(unterf).$
$f^{-1}(B^{\prime })$	$:=x\in A|f(x)\in B^{\prime }$ $Urbild(-menge)von{B}^{\prime }(unterf).$

- Grenzwert von Funktionen:

IMPORTANT

In der Mathematik ist der Limes oder Grenzwert einer Funktion an einer bestimmten Stelle der Wert, dem sich die Funktion in der Umgebung der betrachteten Stelle annähert. Ein solcher Grenzwert existiert jedoch nicht in allen Fällen.

Beispiel

$$f(x)=\frac{1}{x}$$ $$\underset{x\nearrow 0}{\lim }f(x)=\underset{x\nearrow 0}{\lim }-1=-1$$ $$\underset{x\searrow 0}{\lim }f(x)=\underset{x\searrow 0}{\lim }1=1$$

$$\text{linksseitiger Grenzwert:}\underset{x\nearrow a}{\lim }f(x)$$ $$\text{rechtsseitiger Grenzwert:}\underset{x\searrow a}{\lim }f(x)$$

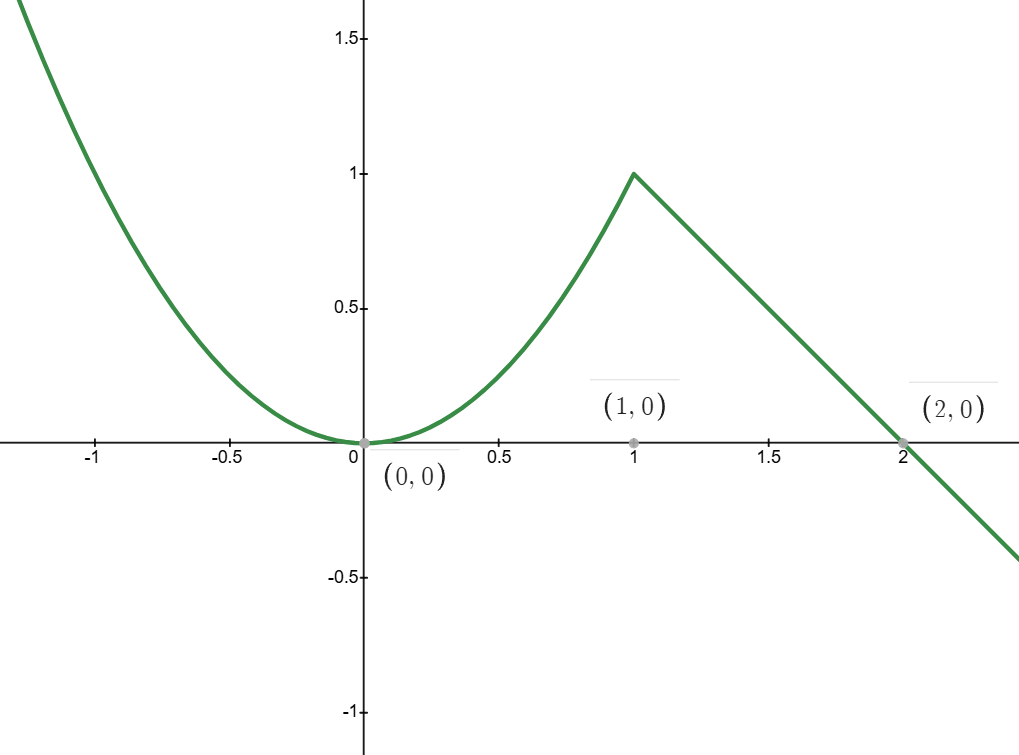
- Stetigkeit einer funktion:

Wichtig

Eine Funktion ist stetig, wenn der Graph der Funktion im Definitionsbereich nahtlos gezeichnet werden kann. Anders ausgedrückt: Der Graph muss in jedem zusammenhängenden Teilintervall aus dem Definitionsbereich nahtlos gezeichnet werden können.
Noch einmal in Worte zusammengefasst bedeutet Stetigkeit von f an einer Stelle a: Sofern a ein innerer Punkt ist prüfen wir ob links– und rechtsseitiger Grenzwert jeweils existieren und auch übereinstimmen. Dann ist die Funktion $f(x)$ an der Stelle x = a stetig.

Beispiel

$$\begin{array}{r}\begin{array}{c}f(x)=\{\begin{array}{ll}{x}^2,& f\ddot{u}rx<1\\ 0,& f\ddot{u}rx=1\\ 2-x& f\ddot{u}rx>1\end{array}\end{array}istnichtstetigdaf(1)=0\end{array}$$

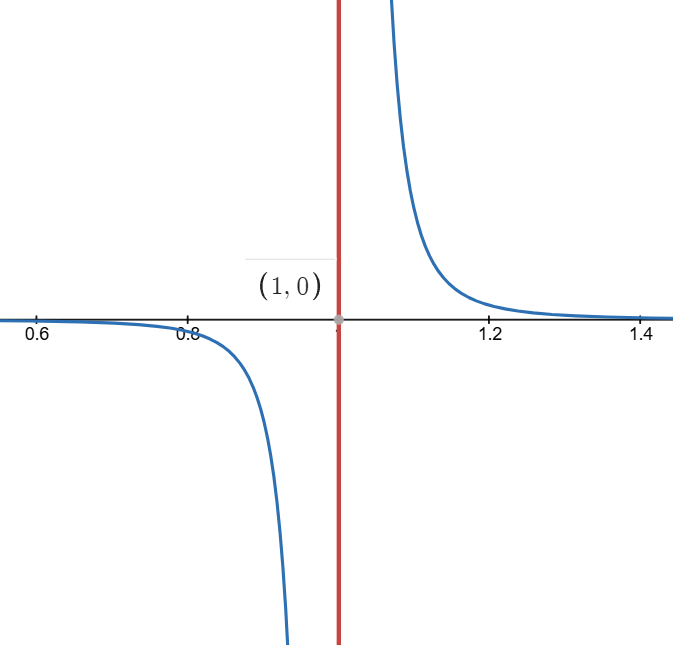
- Polstelle und Lücken

Wichtig

In der Mathematik bezeichnet man eine einpunktige Definitionslücke einer Funktion als Polstelle oder auch kürzer als Pol, wenn die Funktionswerte in jeder Umgebung des Punktes (betragsmäßig) beliebig groß werden. Damit gehören die Polstellen zu den isolierten Singularitäten.

beispiel

$$f(x)=\frac{x^2-1}{(x-1{)}^4}$$

hat den Definitionsbereich ${\mathbb{D}}_f=\mathbb{R}\backslash \{1\}$
Der rechtsseitige Limes liefert:

$$\underset{x\searrow 1}{\lim }\frac{x^2-1}{(x-1{)}^4}=\underset{x\searrow 1}{\lim }\frac{(x-1)(x+1)}{(x-1{)}^4}=\underset{x\searrow 1}{\lim }\frac{(x+1)}{(x-1{)}^3}=\infty$$

und der linksseitige

$$\underset{x\nearrow 1}{\lim }\frac{(x+1)}{(x-1{)}^3}=-\infty$$

---

Ableitungen

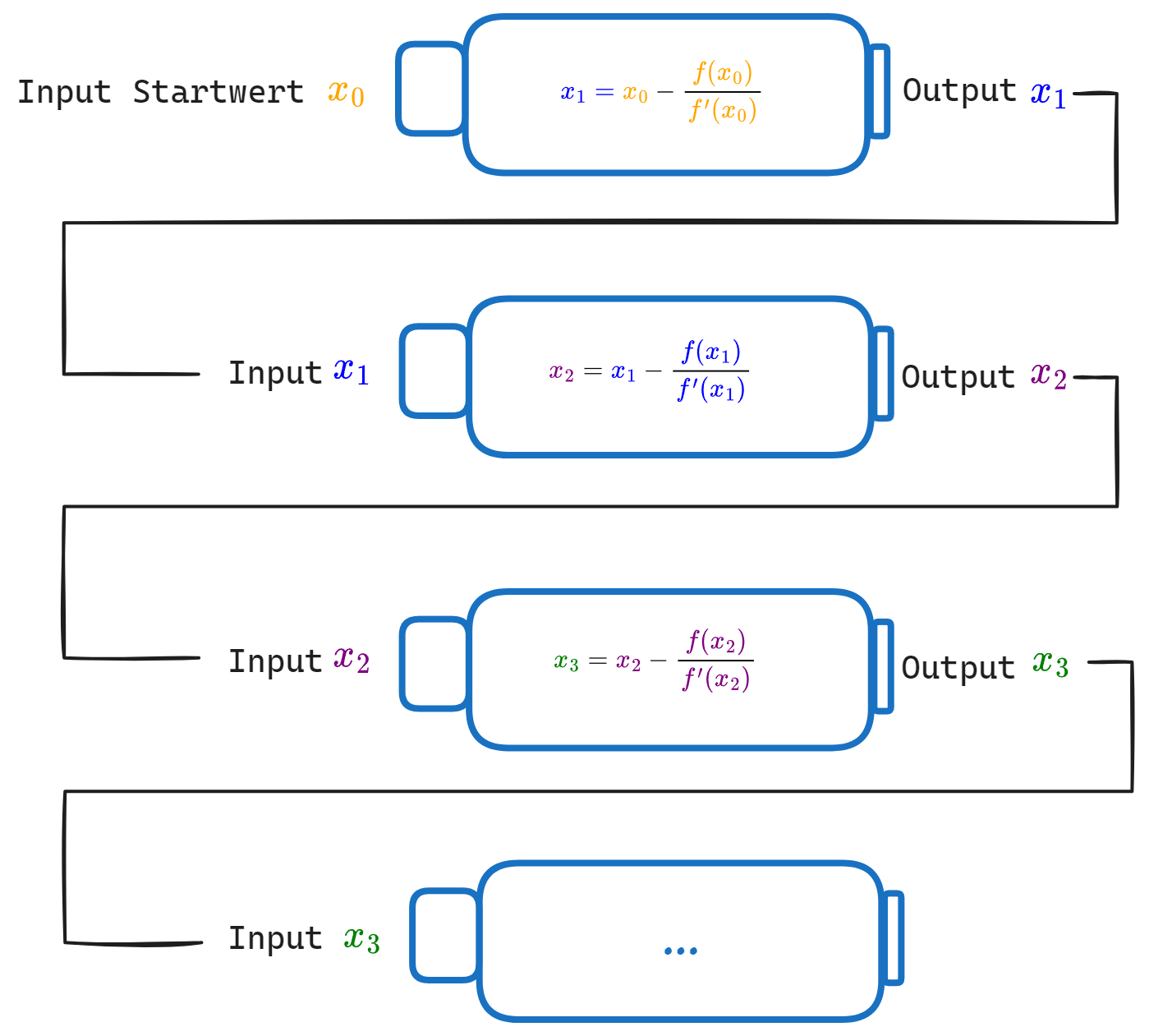
Newton-Verfahren

Wichtig

Das Newton-Verfahren dient zur Annäherung an Nullstellen; durch das immer wieder neu Einsetzen des Ergebnisses in die Newton-Formel nähert man die Nachkommastellen der Nullstelle immer mehr an. Diese Art von Verfahren nennt man Iterationsverfahren.
Iterationsformel:

$$x_{n+1}=x_n-\frac{f(x_n)}{f^{\prime }(x_n)}$$

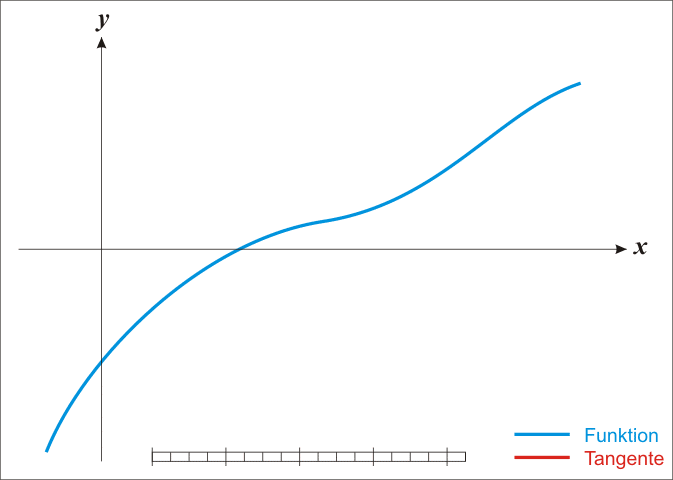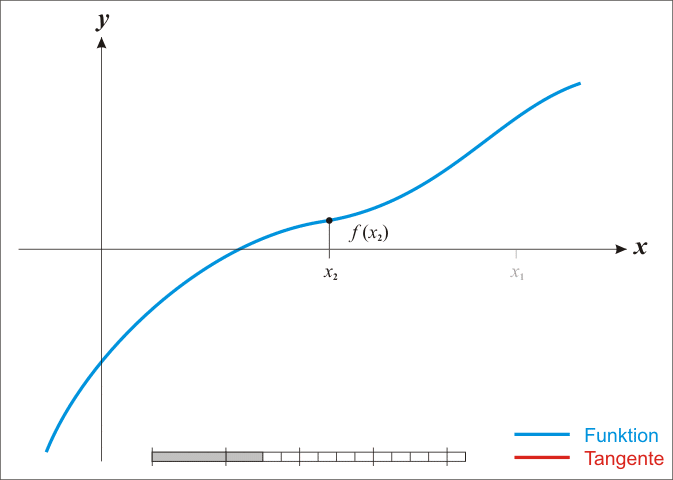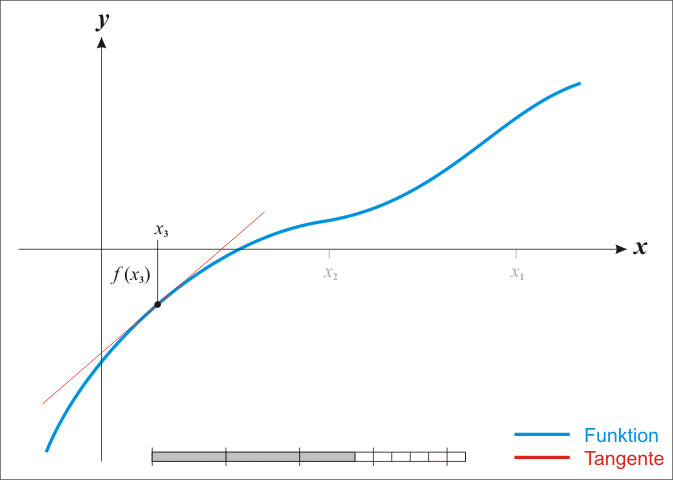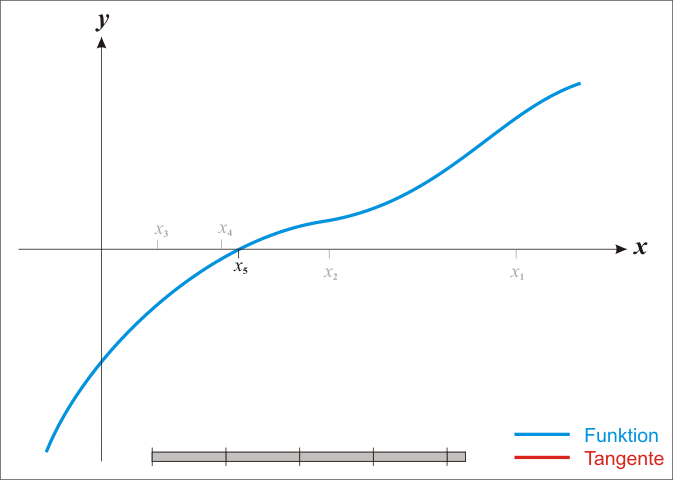
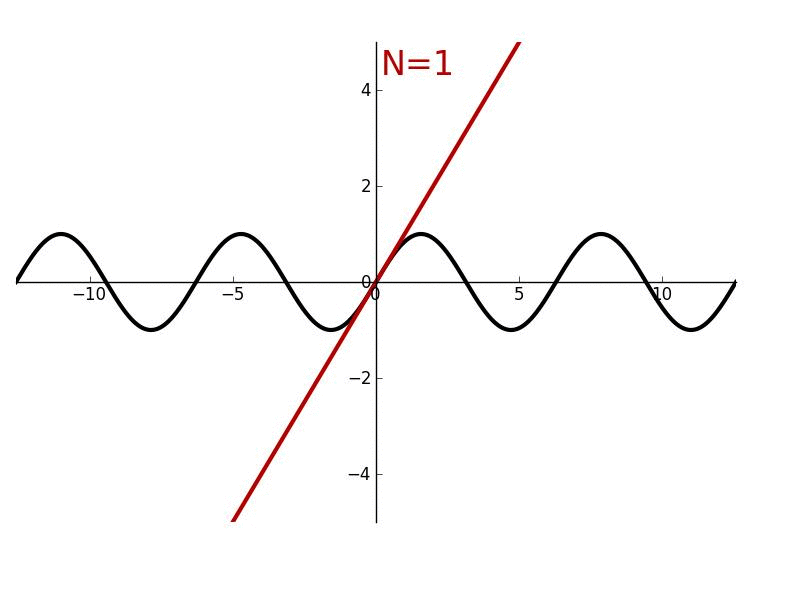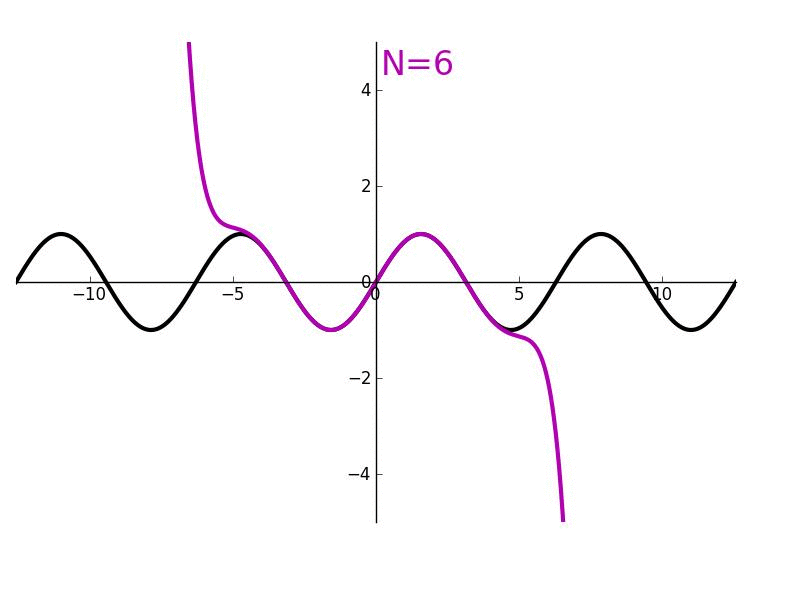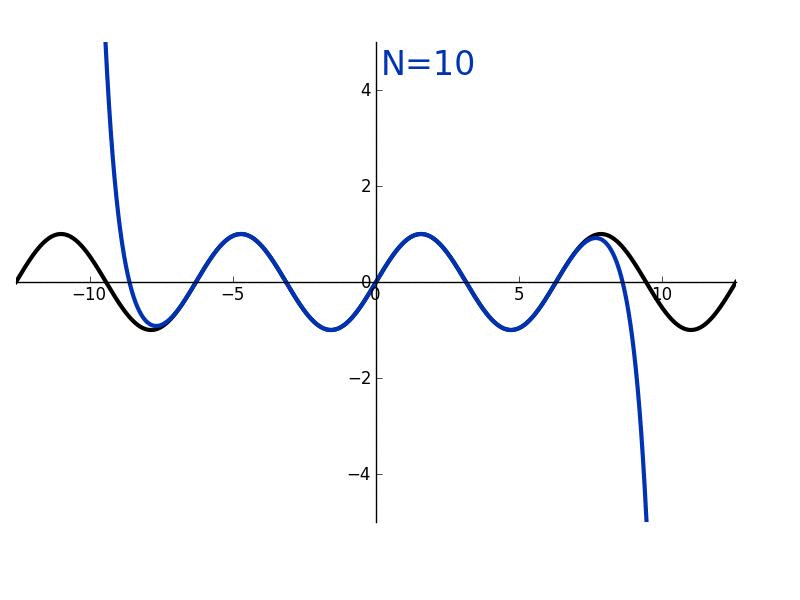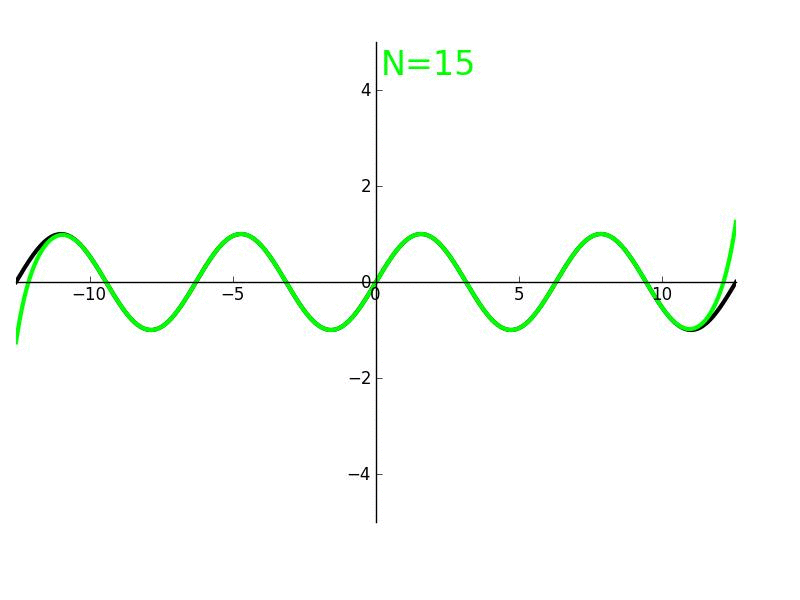
Taylorpolynom

Wichtig

Diesen Prozess können wir an allen Funktionen $f$ fur beliebig viele Ableitungen $n$ durchfuhren, sofern die Funktion an der Stelle $a$ auch $n$-mal differenzierbar ist. Idealerweise lasst sich die $n$-te Ableitung von $f$ formulieren.

$$\sum _{k=0}^n\frac{f^{(k)}(a)}{k!}(x-a{)}^k$$ $$=f(a)+f^{\prime }(a)(x-a)+\frac{f^{(2)}(a)}{2!}(x-a{)}^2+...+\frac{f^{(n)}(a)}{n!}(x-a{)}^n$$

Multivariaten Funktionen

Wichtig

Gegeben ist die Funktion: $u(x,y)$
Die partiellen Ableitungen von u am Punkt $(x,y)\in {\mathbb{R}}^2$ sind gegeben durch

$$\frac{\partial }{\partial x}u(x,y):=\underset{h\to 0}{\lim }\frac{u(x+h,y)-u(x,y)}{h}$$ $$\frac{\partial }{\partial y}u(x,y):=\underset{h\to 0}{\lim }\frac{u(x,y+h)-u(x,y)}{h}$$

Der Gradient einer Funktion u ist gegeben durch

$$\text{grad}(u{)}^T=\nabla u:=\left(\begin{array}{c}{u}_{x_1}\\ ⋮\\ u_{x_n}\end{array}\right).$$

Der Nabla-Operator $\nabla$ und grad beinhalten das Gleiche. Sie unterscheiden sich nur dahingehend ob man die Komponenten in einer Zeile oder einer Spalte zusammenfasst.

Beispiel
Gegeben ist die Funktion:

$$u(x,y)=x^2+x\sin (y)$$

Partiellen Ableitungen von u:

$$\frac{\partial }{\partial x}u(x,y)=2x+\sin (y)$$ $$\frac{\partial }{\partial y}u(x,y)=x\cos (y)$$

Gradient:

$$\nabla u=\left(\begin{array}{c}{u}_x\\ u_y\end{array}\right)=\left(\begin{array}{c}2x+\sin (y)\\ x\cos (y)\end{array}\right).$$

Integration

IMPORTANT

Regeln der unbestimmten Integration:

$$\int u(x)v^{\prime }(x)dx=u(x)v(x)-\int u^{\prime }(x)v(x)dx$$

wo $u(x)$ der “einfache Funktion zum ableiten” ist

Beispiel

$$\begin{array}{rlr}\int \ln xdx& =\int \ln x\cdot 1dx& \\ & =\int u(x)v^{\prime }(x)dx& u(x):=\ln x,v^{\prime }(x):=1\\ & =u(x)v(x)-\int u^{\prime }(x)v(x)dx& u^{\prime }(x)=\frac{1}{x},v(x)=x\\ & =x\ln x-\int \frac{1}{x}xdx& \\ & =x\ln x-x& \\ & =x(\ln x-1)& \end{array}$$

Wichtig

Es sei $F$ eine Stammfunktion von $f$. Man substituiere gemäß $x=g(t)$. Dann ist $dx=g\prime (t)dt$ und es gilt:

$$\int f(x)dx=\int f(g(t))g^{\prime }(t)dt=F(g(t))+C$$

Beispiel

$$\begin{array}{rlr}\int (2-3t{)}^{4}dt& & \\ & =-\frac{1}{3}\int g^{4}dg& \text{Substitution:}g=2-3t\\ & =-\frac{1}{3}\int g^{4}dg& dg=-3dt\\ & =-\frac{1}{15}{g}^5+C& \\ & =-\frac{1}{15}(2-3t{)}^5+C& \end{array}$$